Conference: 10 Years of Algebra at Lincoln
12-14 June 2024

Schedule

The tentative programme will run from Wednesday (12 June) to Friday (14 June), in UK afternoon time to take multiple time zones into account. The preliminary timetable is depicted below: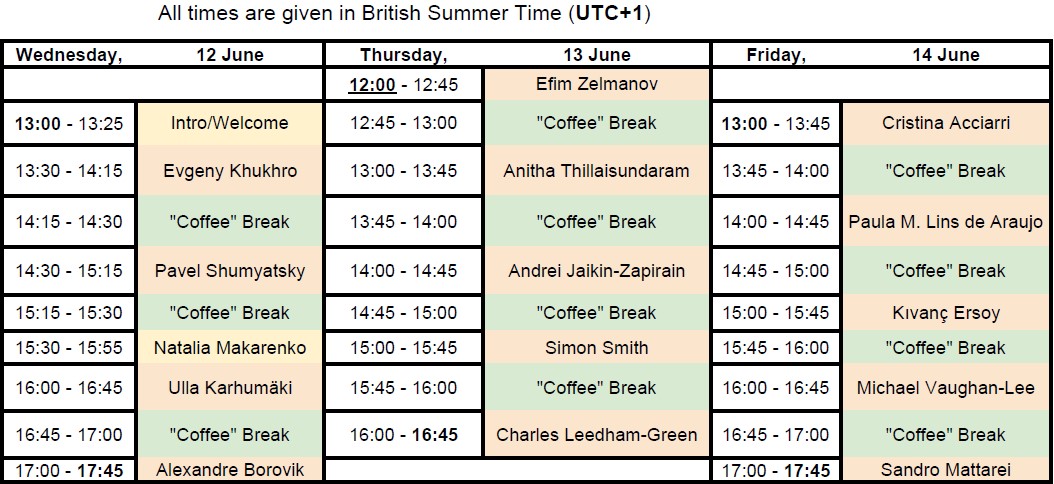

Abstracts

Cristina Acciarri

On groups with automorphisms whose fixed points satisfy Engel-like conditions

Many well-known results in the literature show that, if A is a finite group acting on a finite group G, then the structure of the centralizer \(C_{G}(A)\) of A has influence over the structure of G. The influence is especially strong if the action of A on G is coprime, that is if the orders of A and G are relatively prime.

In this talk we will discuss results that show this phenomenon in the particular situation where, for any nontrivial element \(a \in A\), the centralizers \(C_{G}(a)\) consist of elements satisfying Engel-like conditions.

Alexandre Borovik

Some remarks on teaching algebra and teaching in general

First of all, I wish to use this opportunity to pay tribute to Evgeny Khukhro for his 50 years of work in mathematics education, and to the Algebra Group in the School of Maths and Physics at Lincoln for consistently excellent teaching of Algebra over 10 years of its existence.

I would also try to develop the theme of Evgeny's public lecture of 2018 “Is algebra a spoilsport in mathematics?” by indicating, from my own experience, some ways of showing its beauty and attractiveness.

Kıvanç Ersoy

A generalization of the classical Brauer—Fowler theorem for centralizers of elements of order p

The Brauer—Fowler theorem, a cornerstone of the research on the classification of finite simple groups, states that the order of a finite simple group is bounded uniformly by the orders of its centralizers of involutions. Using the classification of finite simple groups, Hartley proved the following generalized version for any automorphism:
Theorem: There is a function \(f : \mathbb{N} \times \mathbb{N} \to \mathbb{N}\) such that if \(G\) is a finite simple group of order \(n\) with \(k\) many fixed points, then \(|G| \leq f(k,n)\).
As a corollary, Hartley showed that if a locally finite group \(G\) has an element \(x\) of order \(n\) such that \(C_G(x)\) has order \(k\), then \(G\) has a locally solvable normal subgroup of index less than \(f(n, k)\) for the given function \(f\) in the theorem.

Recently, Skresanov proved that if \(G\) is a simple locally finite group and let \(t \in G\) be an involution centralizing at most \(n\) involutions in \(G\), then \(G\) is finite and its order is bounded in terms of \(n\) only. This interesting refinement of the classical Brauer—Fowler theorem replaces the order of the centralizer with the number of involutions centralized, raising the question of whether some generalizations of Hartley's result can be proven.

In this talk, we will present several results about locally finite groups with elements of prime orders centralizing only finitely many elements of given prime or prime power orders.
This is a joint work with Alessandro Dioguardi—Burgio and Edoardo Salati.

Andrei Jaikin-Zapirain

Compressed subgroups in free groups are inert

Let F be a free group. A finitely generated subgroup H is called compressed in F if it is not contained in a subgroup of F of smaller rank than H, and it is called inert in F if \(H \cap U\) is compressed in U for any subgroup U of F. In my talk, I will show that compressed subgroups are also inert. This solves a conjecture of Dicks and Ventura from 1996.

Ulla Karhumäki

Pseudofinite groups of small SU-rank, without CFSG

A pseudofinite group is an infinite group which satisfies every first-order sentence that is true for all finite groups. A simple group is pseudofinite if and only if it is isomorphic to a (twisted) Chevalley group over a pseudofinite field. This celebrated result mostly follows from the work of Wilson in 1995 and heavily relies on the classification of finite simple groups (CFSG). It easily follows that the first-order definable sets of a simple pseudofinite group G are equipped with a notion of dimension, called the SU-rank, taking values in natural numbers. In particular, if \(SU(G)=3\) then G is isomorphic to \(\mathrm{PSL}_2(F)\) for some pseudofinite field F. In this talk we show that the classification \(G \cong \mathrm{PSL}_2(F)\) above does not require CFSG.
This is joint work with Frank Wagner.

Evgeny Khukhro

Local-global rank properties of commutators in finite groups

For a subgroup S of a group G, let \(I_G(S)\) denote the set of commutators \([g,s]=g^{-1}g^s\), where \(g\in G\) and \(s\in S\), so that [G, S] is the subgroup generated by \(I_G(S)\). We prove that if G is a p-soluble finite group with a Sylow p-subgroup P such that any subgroup generated by a subset of \(I_G(P)\) is r-generated, then [G, P] has r-bounded (Prüfer) rank. Examples show that such a result does not hold without the assumption of p-solubility. For an arbitrary finite group G a similar 'global' bound for the rank of [G, P] is proved under a stronger 'local' condition on the ranks of subgroups generated by subsets of \(I_G(P)\) and subgroups generated by subsets of \(I_G(x)\) for \(x\in I_G(P)\).

We also prove that if G is a soluble finite group with a Carter subgroup C such that any subgroup generated by a subset of \(I_G(C)\) is r-generated, then G' = [G, C] has r-bounded rank. Examples show that the assumption of solubility is essential. For an arbitrary finite group G that has a Carter subgroup C, a bound for the rank of G' = [G, C] is obtained involving both the rank of subgroups generated by subsets of \(I_G(C)\) and the maximum rank of composition factors of G isomorphic to \(\mathrm{PSL}_2(q)\) for \(q\equiv 7 (\mathrm{mod}8)\) (work in progress).

An important tool in the proofs is the following result of independent interest: if a finite group G admits a group of coprime automorphisms A such that any subgroup generated by a subset of \(I_G(A)\) is r-generated, then the rank of [G, A] is r-bounded.

This is joint work with Cristina Acciarri, Robert M. Guralnick, and Pavel Shumyatsky.

Charles Leedham-Green

Two ways to tame the class of all finite p-groups

One way two introduce some order into the jungle of finite p-groups is to consider p-groups with p-power automorphism groups of bounded order, and with boundedly many fixed points, and one is by coclass.
I shall concentrate on the latter, and the absurd suggestion that this might lead to a classification of all finite p-groups up to isomorphism.

Paula M. Lins de Araujo

Twisted conjugacy and Reidemeister numbers of certain matrix groups

Twisted conjugacy is a generalisation of usual conjugacy in which one considers a group automorphism \(\varphi : \Gamma \to \Gamma\) and the action \( g \cdot x = g x \varphi(g)^{-1}\) on \(\Gamma\). The orbits of such action are called twisted conjugacy classes (also known as Reidemeister classes).

We will discuss a criterion for certain (infinite) families of matrix groups to have only twisted conjugacy classes of infinite size, which is a group-theoretic property called property \(R_\infty\). This is a joint work with Yuri Santos Rego.

Natalia Makarenko

Lie algebras with Frobenius dihedral groups of automorphisms

I will talk about the recent result on Lie algebras admitting a finite Frobenius group of automorphisms with cyclic kernel and complement of order 2, such that the fixed-point subalgebra with respect to Frobenius kernel is trivial and the fixed-point subalgebra with respect to Frobenius complement is solvable of derived length 2. It turns out that the derived subalgebra of such Lie algebra is nilpotent of class bounded by an absolute constant.

Sandro Mattarei

Graded Lie algebras of maximal class

The title matches that of a series of five papers by various authors from 1997 to 2003, whose goal was the study and classification of such algebras over fields of positive characteristic. I will review motivations and results of those works, including some classifications obtained by Andrea Caranti, Mike Newman, Michael Vaughan-Lee. Then I will describe some generalizations subsequently established with three of my former PhD students.

Pavel Shumyatsky

Groups, rings, and beyond

We will describe some group-theoretical results obtained in a joint work with Evgeny Khukhro.

Simon Smith

Groups acting on trees

Anitha Thillaisundaram

Hausdorff spectrum of p-adic analytic pro-p groups

The concept of Hausdorff dimension first arose in the context of fractals. With time it was also applied to other areas of mathematics, and this was extended in the 90s to profinite groups. A special class of profinite groups includes the p-adic analytic groups, which have a rich geometric and analytic structure, and play a key role in the theory of groups. It is an open question still whether p-adic analytic groups can be characterised by the set of Hausdorff dimensions of their subgroups, i.e. the so-called Hausdorff spectrum. In this talk, we survey what has been done towards answering this question, and we include recent results concerning the Hausdorff spectrum when computed with respect to the lower p-series.
This is joint work with Iker de las Heras and Benjamin Klopsch.

Michael Vaughan-Lee

Engel groups and Engel Lie algebras

I give a summary of results on the local nilpotency of groups satisfying the \(n\)-Engel identity \[ [x,\underbrace{y,y,\ldots ,y}_{n}]=1. \] In the case of locally nilpotent \(n\)-Engel \(p\)-groups I give a summary of some of what is known about their structure. We know from Zelmanov's solution of the restricted Burnside problem that Lie algebras satisfying the \(n\)-Engel identity \[ [x,\underbrace{y,y,\ldots ,y}_{n}]=0 \] are locally nilpotent. Furthermore Zelmanov has also proved that \(n\)-Engel Lie algebras of characteristic zero are globally nilpotent. This implies that \(n\)-Engel Lie algebras of prime characteristic \(p\) are also globally nilpotent for all sufficiently large \(p\). I give a summary of some of what is known about the class of these Lie algebras for \(n \leq 5\), and describe some recent calculations in \(5\)-Engel Lie algebras.

Efim Zelmanov

On growth of Algebras and Formal Languages

We will discuss history and recent results concerning growth functions of groups, algebras, monoids and languages.